Modified theories of gravity and its applications to cosmology and astrophysics
One usually calls modified gravity when the Einstein-Hilbert action is modified/extended. One can modify it by changing the matter/energy (right-hand side of the Einstein field equations) or the parts
related to the geometry (left-hand side of the Einstein field equations). Usually, changing the matter/energy is not considered as being part of modified gravity since the geometrical gravitational theory is the same but new different kinds of sources are considered. This
is an alternative way to understand some issues related to cosmology or astrophysics.
There are different ways of modifying General Relativity. In the below figure one can see a bird's eye view of the spectrum of theories, deviating from GR. Together with the different ways of modifying GR, some of the most important example theories are depicted as well. The figure is drawn by thinking on breaking some of the conditions in the Lovelock's theorem. It turns out that some parts of the figure are connected. For example, some theories which add invariants can be rewritten as scalar-tensor theories. Furthermore, theories can be part of multiple branches of the figure.
For example, quintessence models introduce a scalar field to understand the late-time accelerating behaviour of the Universe. In this perspective, the accelerated expansion at late
times is due to some field sourcing on the right-hand side of the Einstein field equations. This, however, is not the only possible approach to achieve a theoretical description of cosmic acceleration. Another option is to consider cosmic acceleration as a breakdown of general relativity at cosmological scales. In other words, instead of introducing some new matter fluid, one changes the left-hand side of the Einstein field equations, i.e. the pure gravitational sector, in order to obtain the needed late-time accelerated expansion. Modifications of general relativity have a history almost as long as the one of general relativity itself. With the development of the semiclassical approaches
to quantum gravity and, successively, of unification schemes like supergravity and M-theory, it was realised that in many cases low energy versions of these theories correspond to modifications of general relativity, leading to an increased interest in such models, such that nowadays the exploration of modifications of GR occupies a significant part of the research in relativistic gravitation.
I have been interested in studying different modified theories of gravity with the aim of understanding the dark energy and dark matter components of the Universe. The cosmological equations
describing the dynamics of a homogeneous and isotropic Universe are systems of ordinary
differential equations, and one of the most elegant ways these can be investigated is by casting
them into the form of dynamical systems. This allows the use of powerful analytical and
numerical methods to gain a quantitative understanding of the cosmological dynamics derived
by the models under study. We published a long review in this topic in Physics Reports
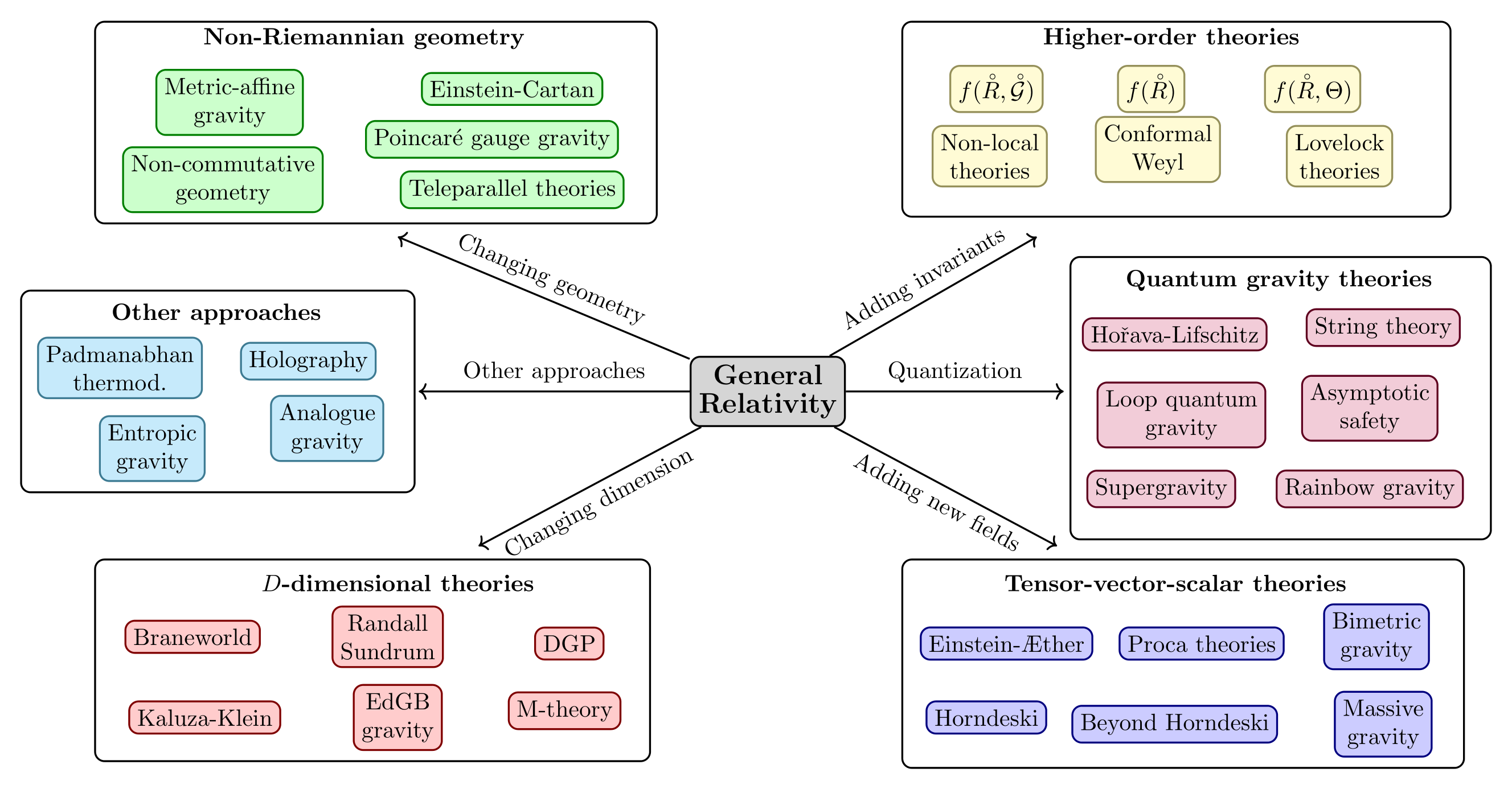Representation of some possible ways of modifying General Relativity
Teleparallel theories of gravity
Soon after the original formulation of this geometrical theory of gravity, it was noted that there exists an alternative
geometrical formulation that is based on a globally flat geometry with torsion. The key mathematical result to
this approach goes back to Weitzenböck who noted that it is indeed possible to choose a connection such that the
curvature vanishes everywhere. This formulation gives equivalent field equations to those of general relativity and we
refer to this as the teleparallel formulation. This naming convention stems from the fact that the notion of parallelism
is global instead of local on flat manifolds.
Clearly, the Einstein-Hilbert action can now be represented in different ways, either using the Ricci scalar or the torsion scalar,
and consequently giving identical equations of motion since the Teleparallel equivalent of GR action is
$$\displaystyle S_{\rm TEGR}={1 \over 16\pi G}\int T e\,\mathrm {d} ^{4}x\;,$$
where $e=\sqrt{-g}=\textrm{det}(e^a{}_\mu)$ and $T$ is the so-called scalar torsion which is related to the Ricci scalar $\bar{R}$ via
$$\bar{R}= -T +\frac{2}{e}\partial_{\mu}(e T^\mu) =-T+B\,.$$
It is easy to notice that the TEGR action gives the Einstein field equations since $T$ and $\bar{R}$ differ by a boundary term $B$. I have been interested in studying such theories and also their extensions in order to see how different they are with respect to the standard modified theories from General Relativity. We wrote a review on Teleparallel gravity and its applications (see
here)
Metric-Affine theories of gravity
One possible route to try to tackle these issues is to extend the role of the geometric structure present in
the theoretical framework towards a full post-Riemannian description of gravity with dynamical metric, torsion and
nonmetricity tensors. Such an extension can be related to the existence of a new fundamental symmetry in nature
by applying the gauge principles not only to the external rotations and translations but also to the scale and shear
transformations, which leads to the formulation of the Metric-Affine Gauge theory of gravity (MAG).
From a geometrical point of view, the standard framework of GR can be consistently formulated as a particular
case of a more general class of metric-affine theories, where the geometry of the space-time is described by a metric,
a coframe and an independent linear connection [4]. Accordingly, the affine connection encodes additional postRiemannian degrees of freedom, which indeed represent the torsion and nonmetricity deformations of an affinely
connected metric space-time
$$T^{\lambda}\,_{\mu \nu}=2\tilde{\Gamma}^{\lambda}\,_{[\mu \nu]}\,,\quad Q_{\lambda \mu \nu}=\tilde{\nabla}_{\lambda}g_{\mu \nu}\,.$$
The components of the affine connection can then be split into independent pieces as follows:
$$
\tilde{\Gamma}^{\lambda}\,_{\mu \nu}=\Gamma^{\lambda}\,_{\mu \nu}+K^{\lambda}\,_{\mu \nu}+L^{\lambda}\,_{\mu \nu}\,,
$$
%
where $K^{\lambda}\,_{\mu \nu}$ is a metric-compatible contortion tensor containing torsion and $L^{\lambda}\,_{\mu \nu}$ a disformation tensor depending on nonmetricity:
$$
K^{\lambda}\,_{\mu \nu}=\frac{1}{2}\left(T^{\lambda}\,_{\mu \nu}-T_{\mu}\,^{\lambda}\,_{\nu}-T_{\nu}\,^{\lambda}\,_{\mu}\right)\,,\quad
L^{\lambda}\,_{\mu \nu}=\frac{1}{2}\left(Q^{\lambda}\,_{\mu \nu}-Q_{\mu}\,^{\lambda}\,_{\nu}-Q_{\nu}\,^{\lambda}\,_{\mu}\right)\,.
$$
The resulting geometric structure is then provided by a metric tensor and an asymmetric affine connection which in general does not preserve the lengths and angles of vectors under parallel transport.
I have been interested on studying different MAG theories and we have obtained black hole solutions within these theories with the torsion and nonmetricity tensor being dynamical.
